Minutová ručička je třikrát delší než sekundová.

Z města A vyjel ráno do města B osobní vlak. Ve stejný okamžik vyjel po stejné trati z města B do města A nákladní vlak. Oba vlaky projely celou trasu stálými rychlostmi. Na trati se vlaky minuly v 9.45. Osobní vlak dojel do cíle v 11.45, nákladní ve 14.15.

Motocykl jede rychlostí 116 km/h, kamion rychlostí 88 km/h. V 7 hodin měl kamion před motocyklem náskok 56 km.

Jolana rozdělovala bonbony. Čtvrtinu snědla, pětinu věnovala kamarádům. Zbytek bonbonů rozdělila na dvě stejné části a ty dala svým bratrům. Bratr Karel dostal 33 bonbonů.

Jana říká Haně. Teď stojí šaty 2 400 Kč. Kdyby je zlevnili o 45 %, potom o 30 % a nakonec o 25 %, byly by zadarmo.

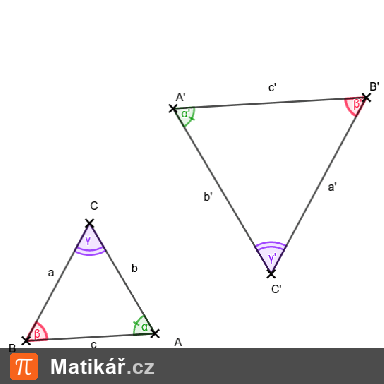
Vypočítej obvod trojúhelníku ABC, pokud víš, že je podobný trojúhelníku EFG, ve kterém |FG| = 144 mm, |EG| = 164 mm, |EF| = 92 mm a poměr podobnosti je 4.
Na letním táboře dělaly děti maketu tábořiště. V jejím středu byl javor, který na maketě měl výšku 28 cm. Ráno vrhal javor stín 14 m dlouhý a jeho maketa měla stín 49 cm dlouhý.

Vzdálenost z Prahy do Olomouce je 250 km. V 6 hod. vyjel z Prahy do Olomouce rychlík rychlostí 85 km/h. Ve stejném okamžiku mu vyjel naproti z Olomouce osobní vlak rychlostí 65 km/h.

Dvě letadla startující současně z letišť A a B letí navzájem proti sobě a minou se za 20 minut. Vzdálenost letišť je 220 km a průměrná rychlost letadla letícího z letiště A je o 60 km/h větší než průměrná rychlost druhého letadla.

Vzdálenost míst A a B je 132 km. V 9 hod. vyjel z místa A cyklista průměrnou rychlostí 24 km/h, v 10 hod. mu vyjel naproti z místa B druhý cyklista průměrnou rychlostí 30 km/h.

V 6 hodin 40 minut vyplul z přístavu parník rychlostí 12 km/hod. Přesně v 10 hodin za ním vyplul ze stejného místa motorový člun rychlostí 42 km/hod.

Místa A a B jsou vzdálena 23 km. Z místa A vyšel chodec průměrnou rychlostí 4 km/hod. O 45 minut později vyjel proti němu z místa B cyklista průměrnou rychlostí 16 km/hod.

V hotelu bydlí polovina lidí v prvním patře, třetina ve druhém patře a zbylých 40 hostů v podkroví. Hotel je obsazen ze 75 %.

Zájezd byl zdražen o šestinu a po zdražení stál 4 200 Kč.

Z krajského města vyjede v 9 hodin 30 minut automobil rychlostí 40 km/hod. V 11 hod. téhož dopoledne za ním vyjede motocykl rychlostí 60 km/hod.

Seriál je o 15 minut kratší než pohádka, ale o 20 minut delší než dokumentární film. Všechny tři pořady trvají dohromady 175 minut.

Adam je o 8 let starší než Bertík, Bertík je o 2 roky starší než Cyril. Dohromady je chlapcům 27 let.

V 6 hodin 30 minut vyplul z přístavu parník plující rychlostí 12 km/hod. Přesně v 10 hodin za ním vyplul motorový člun, který plul konstantní rychlostí 40 km/hod.

Průměrně se ze 100 litrů mléka vyrobí 16 litrů smetany a ze 100 litrů smetany se vyrobí 20 litrů másla.

