Krabice má výšku 55 cm a šířku 40 cm. Objem krabice je 180 litrů.

Ve městě Náhoda zrušily jízdní řády a autobusy MHD jezdí zcela náhodně. Představte si, že stojíte na zastávce, na které zastavuje 5 autobusů s čísly 12, 14, 15, 21 a 27 a vy se dvěma z nich můžete dostat domů.

Plat pracovníka byl zvýšen o 8 % nyní je 14 580 Kč.

Je potřeba převézt zlaté cihly o rozměrech 20 × 15 × 8 cm autem, které má nosnost 3,5 t.
Hustota zlata je 19,3 .

Na jednu rybičku v akváriu je doporučené mít 3 litry vody. Akvárium má rozměry dna 80 × 50 cm a výškou 45 cm. Hladina vody sahá do výšky 5 cm pod horní okraj akvária.

Palačinku si můžete dát s malinovou, jahodovou, nebo jablečnou náplní. Můžete si ji dát bez polevy, s karamelovou, nebo čokoládovou polevu. Také si můžete nebo nemusíte dát na palačinku šlehačku.

V železářství prodávali 1 kg hřebíků za 400 Kč a 1 kg vrutů za 800 Kč. Celkem prodali 5 kg a utržili 3 200 Kč.

Na účtu v bance bylo 6 600 Kč, za což byl na konci roku připsán úrok 330

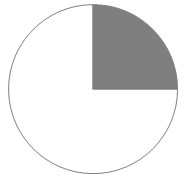
V grafu jsou tmavou barvou vyznačeny části celku.



Patrik, Pavel, Alena a Renata šli do divadla.

V divadle je 60 % dospělých a zbytek dětí. Z dospělých je žen a 18 mužů.

Zahradnice měly zasadit 200 sazenic. Lenka zasadila o 20 % více než Dana. Eva zasadila o 40 více než Dana. Zuzka zasadila toho co Dana.

V cukrárně mají 10 druhů zákusků, 8 druhů zmrzliny a 3 druhy kávy.

Šachového turnaje se zúčastnilo 5 hráčů. Hrál každý s každým dvakrát.




Je dán pravidelný šestiúhelník ABCDEF.

Na houpačce, kterou je páka se dvěma rameny, sedí dvě děti. Houpačka je v rovnováze. Na levé straně sedí 150 cm od středu dítě s hmotností 30 kg a na pravé dítě s hmotností 20 kg.

Olga jela na projížďku na kole. Za hodinu se za ní po stejné trase vypravil bratr na motorce stálou rychlostí 60 km/h a dojel ji za hodiny.
