Úlohy: 21–40 / 322

12345
Přehled ročníků

21. Lineární rovnice

Vyřešte lineární rovnice
a)   \[ \frac{2x + 6}{4} = 3 \]
b)   \[ \frac{3x - 9}{6} = x - 2 \]
c)   \[ \frac{x + 5}{2} + \frac{x - 3}{4} = 3 \]
d)   \[ \frac{4x + 8}{6} = \frac{2x}{3} + 2\]
e)   \[ \frac{3x - 9}{4} = \frac{x + 3}{2}\]
f)   \[ \frac{5x + 15}{8} = \frac{3x}{4} + 1\]
Řešení
a)   \( x = 3 \)
b)   \( x = 1 \)
c)   \( x = 5 \)
d)   nemá řešení
e)   \( x = 15 \)
f)   \( x = 7 \)
Matematická úloha – Lineární rovnice

22. Lineární rovnice

Vyřešte lineární rovnice a proveďte zkoušku:
a)   \( 2(x + 3) = 16 \)
b)   \( 5(x - 2) + 3 = 3x + 9 \)
c)   \( 4(x + 1) = 2(x + 7) \)
d)   \( 3(x - 5) - 2 = x - 4 \)
e)   \( 6(x + 2) = 6x + 15 \)
f)   \( 3(x + 4) - 2x = 6 \)
Řešení
a)   \( x = 5 \)
b)   \( x = 8 \)
c)   \( x = 5 \)
d)   \( x = 6.5 \)
e)   nemá řešení
f)   \( x = -6 \)
Matematická úloha – Lineární rovnice

23. Nákup pečiva

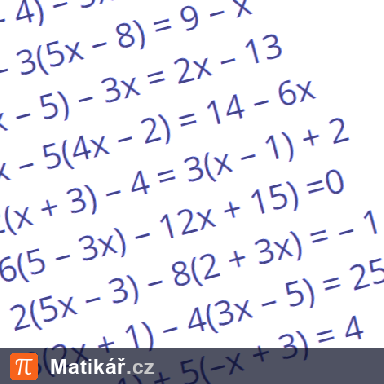
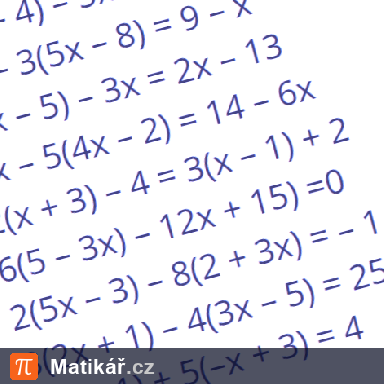
Veka stojí třikrát více než houska. Chleba stojí čtyřikrát více než veka. Pavel koupil dva chleby, tři veky a pět housek. Za tento nákup zaplatil 152 Kč.

Vypočítejte:
a)   kolik stála jedna houska,
b)   kolik stála jedna veka,
c)   kolik stál jeden chleba.
Řešení
a)   Cena jedné housky je 4 Kč,
b)   Cena jedné veky je 12 Kč,
c)   Cena jednoho chleba je 48 Kč.
Matematická úloha – Nákup pečiva

24. Průsečíky s osami

Vypočítejte průsečíky s osou \(x\) a osou \(y\) u grafů následujících funkcí.
a)   \( y = 2x - 6 \)
b)   \( y = -3x + 9 \)
c)   \( y = \frac{1}{2}x - 4 \)
d)   \( y = -5x + 15 \)
e)   \( y = 4x + 8 \)
f)   \( y = 7x \)
g)   \( y = 5 \)
h)   \( y = -2x + 10 \)
Řešení
a)   \( P_x = [3, 0]; P_y = [0, -6]; \)
b)   \( P_x = [3, 0]; P_y = [0, 9]; \)
c)   \( P_x = [8, 0]; P_y = [0, -4]; \)
d)   \( P_x = [3, 0]; P_y = [0, 15]; \)
e)   \( P_x = [-2, 0]; P_y = [0, 8]; \)
f)   \( P_x = [0, 0]; P_y = [0, 0]; \)
g)   \( P_{x} \text{ neexistuje}; P_y = [0, 5]; \)
h)   \( P_x = [5, 0]; P_y = [0, 10]; \)
Matematická úloha – Průsečíky s osami

25. Přečtená kniha

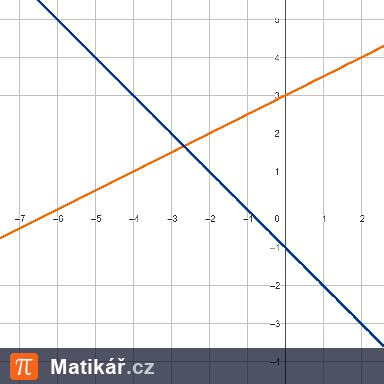
Adéla plánovala přečíst knihu za 6 dní. Nakonec ji ale přečetla za 5 dní, protože každý den přečetla o 4 víc, než plánovala.

Vypočítejte, kolik má kniha stran.
Řešení
Kniha má 120 stran.
Matematická úloha – Přečtená kniha

26. Nákup čokolády

Velká čokoláda stojí o třetinu více než malá čokoláda. Dvě velké a tři malé čokolády stojí 255 korun. Vedoucí koupili dětem na tábor o 10 více malých čokolád než velkých čokolád a zaplatili za ně celkem 1 710 korun.

Vypočítejte:
a)   kolik stála malá čokoláda,
b)   kolik stála velká čokoláda,
c)   kolik vedoucí koupili malých čokolád,
d)   kolik vedoucí koupili velkých čokolád.
Řešení
a)   Malá čokoláda stojí 45 korun.
b)   Velká čokoláda stojí 60 korun.
c)   Vedoucí koupili 12 velkých čokolád.
d)   Vedoucí koupili 22 malých čokolád.
Matematická úloha – Nákup čokolády

27. Limonády v obchodě

Limonáda se prodává v malých a velkých lahvích. Malá láhev má objem 7 dl, velká 12 dl. V obchodě je velkých láhví o 10 méně než malých a celkem v nich je 469 dl limonády.

Vypočítejte, kolik je v obchodě:
a)   malých limonád,
b)   velkých limonád.
Řešení
a)   V obchodě je 31 malých lahví
b)   V obchodě je 21 velkých lahví.
Matematická úloha – Limonády v obchodě

28. Děti a dospělí v kině

Dětský lístek do kina stál 100 korun, dospělácký stál 150 korun. V kině bylo celkem 37 návštěvníků a tržba za lístky byla 4 850 korun.

Vypočítejte, kolik bylo v kině:
a)   dětí,
b)   dospělých.
Řešení
a)   V kině bylo 14 dětí.
b)   V kině bylo 23 dospělých.
Matematická úloha – Děti a dospělí v kině

29. Pavlův výlet

Pavel jel na třídenní cyklistický výlet. První den ujel 30 % cesty. Druhý den ujel 60 % zbytku cesty. Třetí den ujel zbylých 56 km.

Vypočítejte, kolik kilometrů dlouhý byl Pavlův výlet.
Řešení
Pavlův výlet byl dlouhý 200 kilometrů.
Matematická úloha – Pavlův výlet

30. Zdražení televizoru

Televizor byl zdražen o 20 % a poté ještě jednou, tentokrát o 25 %. Nyní stojí 13 200 korun.

Vypočítejte:
a)   kolik korun stál televizor před prvním zdražením,
b)   o kolik procent byl televizor celkově zdražen.
Řešení
a)   Před prvním zdražením stál televizor 8 800 korun.
b)   Celkově byl televizor zdražen o 50 %.
Matematická úloha – Zdražení televizoru

31. Bonbóny na regálu

Velký sáček bonbónů stojí 25 korun, malý sáček stojí 15 korun. V regálu jsou bonbóny celkem za 1 900 korun. Malých sáčků je o 12 více než velkých.

Vypočítejte, kolik bylo na regálu:
a)   malých sáčků,
b)   velkých sáčků.
Řešení
a)   Na regálu bylo 55 malých sáčků,
b)   na regálu bylo 43 velkých sáčků.
Matematická úloha – Bonbóny na regálu

32. Lichoběžníkový příkop

Příkop má profil lichoběžníku. Je dlouhý 10 m, vysoký 60 cm, dno je široké 20 cm a u vršku je šířka 30 cm.

Vypočítejte, kolik litrů vody se do příkopu vejde.
Řešení
Do příkopu se vejde 1 500 litrů vody.
Matematická úloha – Lichoběžníkový příkop

33. Návštěvníci městské knihovny

Ve městě proběhl průzkum, který ukázal, že v roce 2 023 navštěvovalo knihovnu 60 % obyvatel. V roce 2 024 se v dalším průzkumu ukázalo, že knihovnu navštěvovalo o 25 % více, tedy 7 200 obyvatel. Počet obyvatel města se nezměnil.

Vypočítejte:
a)   kolik má město obyvatel,
b)   kolik procent obyvatel města navštěvovalo knihovnu v roce 2 024.
Řešení
a)   Město má 9 600 obyvatel.
b)   V roce 2 024 knihovnu navštěvovalo 75 % obyvatel města.
Matematická úloha – Návštěvníci městské knihovny

34. Peníze Radka a Simony

Kdyby měl Radek o 50 korun méně, měl by o třetinu více než Simona. Oba dohromady mají 1 520 korun.

Vypočítejte, kolik korun má:
a)   Radek,
b)   Simona.
Řešení
a)   Radek má 890 korun,
b)   Simona má 630 korun.
Matematická úloha – Peníze Radka a Simony

35. Mince v sáčku

V sáčku jsou jen 2korunové a 10korunové mince, celkem tam je 46 mincí. V sáčku je 196 korun.

Vypočítejte, kolik je v sáčku:
a)   dvoukorunových mincí,
b)   desetikorunových mincí.
Řešení
a)   V sáčku je 33 dvoukorunových mincí.
b)   V sáčku je 13 desetikorunových mincí.
Matematická úloha – Mince v sáčku

36. Peníze tří dívek

Nela, Olga a Petra mají celkem 7 500 korun. Olga má dvakrát víc než Nela. Kdyby měla Petra o 500 korun víc, měla by stejně jako Olga.

Vypočítejte, kolik korun má:
a)   Nela,
b)   Olga,
c)   Petra.
Řešení
a)   Nela má 1600 korun,
b)   Olga má 3200 korun,
c)   Petra má 2700 korun.
Matematická úloha – Peníze tří dívek

37. Túra tří kamarádů

Každý ze tří kamarádů šel na víkendovou túru. Dohromady ušli 84 kilometrů. Karel ušel dvakrát více než Libor. Martin ušel dvakrát méně než Libor.

Vypočítejte, kolik ušel:
a)   Karel,
b)   Libor,
c)   Martin.
Řešení
a)   Karel ušel 48 kilometrů,
b)   Libor ušel 24 kilometrů,
c)   Martin ušel 12 kilometrů.
Matematická úloha – Túra tří kamarádů

38. Jahodové a smetanové nanuky

V prodejně měli jen jahodové a smetanové nanuky. Jahodových nanuků bylo v prodejně o třetinu více než smetanových nanuků. Celkem měli v prodejně 420 nanuků.

Určete, kolik bylo v prodejně:
a)   jahodových nanuků,
b)   smetanových nanuků.
Řešení
a)   V prodejně bylo 240 jahodových nanuků
b)   a 180 smetanových nanuků.
Matematická úloha – Jahodové a smetanové nanuky

39. Paření na mobilu

Karel pařil na telefonu o 240 minut více než Libor, takže pařil 3krát více času.

Vypočítejte, kolik minut pařil Libor.
Řešení
Libor tedy pařil 120 minut.
Matematická úloha – Paření na mobilu

40. Peníze Ivana a Jany

Ivan má 4krát více peněz než Jana. Oba dva dohromady mají 280 korun.

Vypočítejte, kolik korun má Jana.
Řešení
Jana tedy má 56 korun.
Matematická úloha – Peníze Ivana a Jany
 
12345