
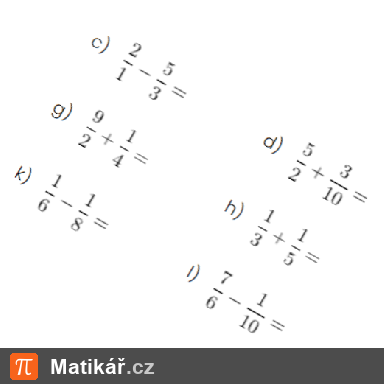
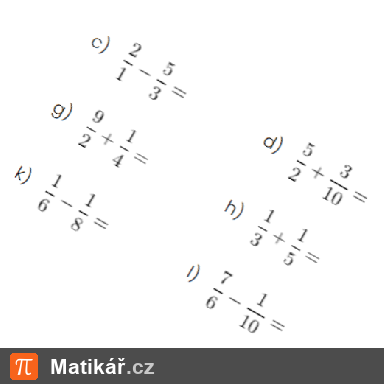
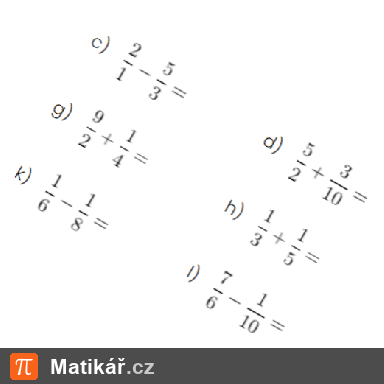
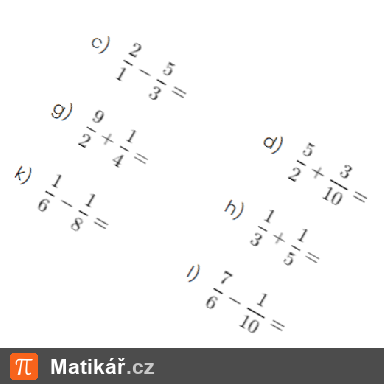
Pavlínka s Klárkou mají dohromady 34 bonbonů. Když dá Klárka Pavlínce 2 bonbony, budou mít stejně.

Uršula uplavala o dvě pětiny bazénů více než Kamila. Obě dívky dohromady uplavaly 1 800 m. Bazén má délku 50 metrů.

Tomáš měl v akváriu měl 12 rybiček, což bylo o tři pětiny méně rybiček než měla Dana.

Když vynásobím dvě stejná přirozená čísla, dostanu stejný výsledek, jako když je sečtu.

V sadě roste celkem 18 hrušní a jabloní. Hrušní je 2krát méně než jabloní.

Pole má na plánku s měřítkem 1:16000 má rozměry 2 cm × 5 cm.

Na běžném balíku papírů do tiskáren a kopírek je štítek s údajem 80 g/m2, což znamená, že jeden metr čtverečný takového papíru váží 80 g.

Na čtyři porce je třeba nachystat 420 g masa. Budeme ale připravovat o tři porce více.

Vytvoření 4 výrobků trvá celkem 80 hodin. Každý výrobek vyrábějí stejně dlouho.

Jedna strana obdélníku má délku 18 cm. Obvod obdélníku je 48 cm.
Učebna má délku 12 m, šířku 6,50 m a výšku 4 m a je třeba vymalovat. Cena malování je 50 Kč za 1 m2.

Pokud k dvojnásobku neznámého čísla připočteme 17, dostaneme 67.
Pokud k polovině neznámého čísla připočteme 6 000 dostaneme 9 000.

Martina a Alena mají dohromady 114 bonbónů. Martina má 5krát více než Alena.

Petr se učil o čtvrtinu času více než Simona. Dohromady se učili 2 hodiny a 51 minut.
